📂Banach Space

Infinite-Dimensional Vector Spaces and Schauder Bases

Definition¹

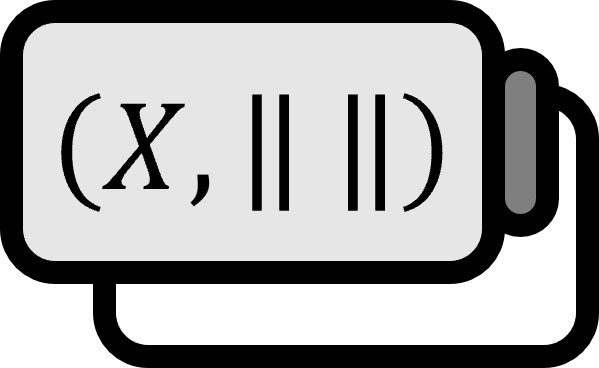
Let’s call $(X, \left\| \cdot \right\|)$ a normed space. If there exists a unique sequence of scalars $\left\{ a_{k} \right\}_{k \in \mathbb{N}}$ that satisfies the following for every element $\mathbf{x}\in X$ in $X$, then $\left\{ \mathbf{e}_{k} \right\}_{k \in \mathbb{N}} \subset X$ is called the Schauder basis of $X$.

$$ \mathbf{x}= \sum_{k \in \mathbb{N}} a_{k} \mathbf{e}_{k} $$

Description

The basis of a vector space is called the Schauder basis, especially when discussing ‘infinite’ linear combinations. Since it deals with infinity, it is closely related to properties of Banach spaces, and especially for Hilbert spaces, the following useful theorem is known.

Equivalent Conditions for an Orthonormal Basis: Let’s say $H$ is a Hilbert space. For the orthonormal system $\left\{ \mathbf{e}_{k} \right\}_{k \in \mathbb{N}} \subset H$ of $H$, the following are all equivalent.

• (i): $\left\{ \mathbf{e}_{k} \right\}_{k \in \mathbb{N}} \subset H$ is an orthonormal basis of $H$.
• (ii): For all $\mathbf{x}\in H$, $$ \mathbf{x}= \sum_{k \in \mathbb{N}} \langle \mathbf{x}, \mathbf{e}_{k} \rangle \mathbf{e}_{k} $$
• (iii): For all $\mathbf{x}, \mathbf{y} \in H$, $$ \langle \mathbf{x}, \mathbf{y} \rangle = \sum_{k \in \mathbb{N}} \langle \mathbf{x}, \mathbf{e}_{k} \rangle \langle \mathbf{e}_{k} , \mathbf{y} \rangle $$
• (iv): For all $\mathbf{x}\in H$, $$ \sum_{k \in \mathbb{N}} \left| \langle \mathbf{x}, \mathbf{e}_{k} \rangle \right|^{2} = \left\| \mathbf{x}\right\|^{2} $$
• (v): $\overline{\text{span}} \left\{ \mathbf{e}_{k} \right\}_{k \in \mathbb{N}} = H$
• (vi): If $\mathbf{x}\in H$ and for all $k \in \mathbb{N}$, $\langle \mathbf{x}, \mathbf{e}_{k} \rangle = 0$ implies $\mathbf{x}= \mathbf{0}$

See also

• Basis of a finite-dimensional vector space: Hamel basis