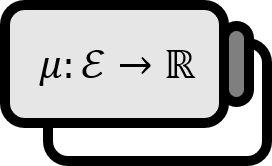Convergence in Measure

Definition

Let space $S$ be both a metric space $( S , \rho)$ and a measurable space $(S,\mathcal{B}(S))$.

Measure Theory

When a measure $\mu$ defined on $S$ and a sequence of measures $\left\{ \mu_n \right\}_{n \in \mathbb{N}}$ is $n \to \infty$, it is said to converge weakly to measure $\mu$ if it satisfies the following for all $f \in C_{b}(S)$: $$ \int_{S} f d\mu_{n} \to \int_{S} f d\mu $$ It is denoted as $\mu_{n}\overset{W}{\to}\mu$.

Probability Theory

When a probability $P$ and a sequence of probabilities $\left\{ P_n \right\}_{n \in \mathbb{N}}$ defined on $S$ is $n \to \infty$, it is said to converge weakly to probability $P$ if it satisfies the following for all $f \in C_{b}(S)$: $$ \int_{S} f dP_{n} \to \int_{S} f dP $$ It is denoted as $P_{n}\overset{W}{\to}P$.

$C_{b}(S)$ represents the set of bounded continuous functions defined on $S$ as follows: $$ C_{b}(S) := \left\{ f:S \to \mathbb{R} \mid f\text{ is bounded and continuous} \right\} $$
$\displaystyle \int_{S} f dP$ can be simply denoted as $\displaystyle Pf := \int_{S} f dP$.

Description

A primary application of the weak convergence of measures is in probability theory. This post is written assuming readers who are familiar with statistics rather than those new to topology. If your background is in mathematics, you can comfortably read about topology and see what aspects of it are needed in probability theory.

Statistics

In fact, weak convergence of probabilities (measures) can be seen as convergence in distribution explained by measure theory. Convergence in distribution encountered in mathematical statistics, for a single variable probability variable, is said to be $X_{n} \overset{D}{\to} X$ when there exists a cumulative distribution function $F_{X_{n}}$ for $X_{n}$ so that for every point $x \in X$ where the cumulative distribution function $F_{X}$ is continuous, the following condition is met: $$ \lim_{n\to\infty} F_{X_{n}}(x) = F(x) $$ Note that the above two formulas are similar in satisfying the condition for all $f \in C_{b}(S)$. $$ \lim_{n\to\infty} P_{n} f = P f $$ Do not think of a sequence of probabilities (measures) as something difficult; first approach it intuitively. The formula indicates that $f$ converges to $P f$ with a weight of $P_{n}$. The functions dealt with in probability theory are ultimately random variables, which could possibly be represented as $X_{n}\equiv P_{n}f$, $X \equiv Pf$. $$ X_{n} \overset{D}{\to}X \overset{?}{\iff} P_{n} \overset{W}{\to} P $$ What is not visible in the left formula is every point $x \in S$ where $X$ is continuous, and in the right formula, it’s every bounded continuous function $f \in C_{b}(S)$.

Topology

To discuss weak convergence, it is essential to be familiar with basic topology. Fortunately, spaces discussed in measure theory are quite intuitive, so knowing about metric spaces is sufficient for now. That space $S$ being both a metric space $( S , \rho)$ and $(S,\mathcal{B}(S))$ a measurable space means that $S$ contains the smallest sigma field that includes all open balls $B_{\rho}(x , \varepsilon) := \left\{ y \in S : \rho (x,y) < \varepsilon \right\}$ created by distance function $\rho$ for all $x \in S$ and all $\varepsilon>0$, i.e., the Borel sigma field $\mathcal{B}(S)$.

Open sets are unions of open balls, and by the nature of sigma fields, their complements are also included in $\mathcal{B}(S)$, meaning all closed sets must also belong to $\mathcal{B}(S)$. For a simple example, consider $S=\mathbb{R}$; $\mathcal{B}(\mathbb{R})$ consists of the following open and closed sets: $$ \emptyset, \mathbb{R}, [0,7], (-\infty, \pi) , \left\{ 1 \right\}, (-1,1) \cap (0,9) $$ Moreover, according to other conditions of sigma fields, the following sets with mixed open and closed properties are also included. It would be nice to feel that the mentioned sets here are relatively intuitive. $$ [0,1), (-\infty,\pi], [\pi , \infty) , \left\{ 1 \right\} \cup (-3,-2) $$ If you still find it difficult and cannot accept the definitions, it is recommended to study topology when you have the time. Of course, starting with topology to study probability theory might seem inefficient. But it’s not about efficiency; the experience itself can be very beneficial. Topology has many shocking, perverse, and extreme examples that abound. Experiencing the spicy taste of abstract mathematics will make you appreciate studying nice spaces like metric spaces and help develop a mathematical sense.

Here is a useful theorem regarding this topic:

Theorem

Let $P$ be a probability defined in $(S,\mathcal{B}(S))$. Then there exist closed sets $F_{\varepsilon}$ and open sets $G_{\varepsilon}$ that satisfy the following for all $A \in \mathcal{B}(S)$ and $\varepsilon>0$: $$ F_{\varepsilon}\subset A \subset G_{\varepsilon} \\ P ( G_{\varepsilon} \setminus F_{\varepsilon}) < \varepsilon $$ Based on this theorem, the following corollary can be obtained: $$ \begin{align*} P(A) =& \sup \left\{ P(F) : F \in \mathcal{B}(S) \text{ is closed in S} \right\} \\ =& \inf \left\{ P(G) : G \in \mathcal{B}(S) \text{ is open in S} \right\} \end{align*} $$

Needless to say, since any topological space was originally $A^{\circ} \subset A \subset \overline{A}$, it must be possible to assert the existence of slightly smaller open sets and slightly larger closed sets than $A$, but it’s not as obvious that there exist slightly smaller closed sets and slightly larger open sets that satisfy $P ( G_{\varepsilon} \setminus F_{\varepsilon}) < \varepsilon$. This becomes apparent after confirming that probability $P$ is continuous because it is a measure.

Indeed, looking at the above picture might be easier to understand than hearing a hundred words. This property enables finding a narrow band to navigate around the boundary $\partial A$ of $A$ whenever $\varepsilon > 0$ is given.