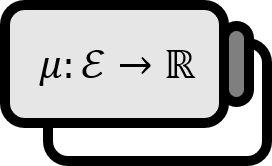📂Measure Theory

Vitali Convergence Theorem

Theorem ¹

Let’s assume that a measure space $( X , \mathcal{E} , \mu)$ is given.

When we say $1 \le p < \infty$, the sequence of functions $\left\{ f_{n} \right\}_{n \in \mathbb{N}} \subset \mathcal{L}^{p}$ converging to $f$ in $\mathcal{L}_{p}$ is equivalent to the necessity and sufficiency of all three conditions being satisfied:

• (i): $\left\{ f_{n} \right\}$ converges in measure to $f$.
• (ii): $\left\{ | f_{n} |^{p} \right\}$ is uniformly integrable.
• (iii): For all $\varepsilon > 0$, $$ F \in \mathcal{E} \land F \cap E = \emptyset \implies \int_{F} | f_{n} |^{p} d \mu < \varepsilon^{p} \qquad \forall n \in \mathbb{N} $$ is satisfied, and there exists $E \in \mathcal{E}$ such that $\mu (E) < \infty$.

Description

• (iii): This might sound complicated, but $E$ needs to be dependent on some $\varepsilon>0$ such that it can be expressed as $E = E_{\varepsilon}$ without being too large to satisfy $\mu (E) < \infty$. There must exist $E_{\varepsilon}$ small enough not to overlap with a sufficiently large $F$ that satisfies $\displaystyle \int_{F} | f_{n} |^{p} d \mu < \varepsilon^{p}$.
  In fact, as long as the inequality is satisfied, $E$ can grow indefinitely without any issue. Therefore, this condition is trivially met if the measure $\mu$ is a finite measure. Since $\mu (X) < \infty$ for the entire space $X$, setting $E_{\varepsilon} = X$ means there’s only one measurable set that doesn’t overlap, which is $\emptyset \in \mathcal{E}$, and so $\displaystyle \int_{\emptyset} | f_{n} |^{p} d \mu = 0$ makes it unnecessary to check the condition.

An example of a finite measure is probability $P$. In the theory of probability, Vitali’s convergence theorem becomes one that extends the notion of convergence to $\mathcal{L}_{p}$ by adding the criterion of uniform integrability.